期权定价的几种方法

LiuKK

Jun 25, 2016

阅读本文需要 18 分钟

这里的公式显示有问题，请移步我在优矿上的帖子：期权定价的几种方法

1.Black-Scholes期权定价公式的推导

保罗萨缪尔森在1965年提出来的股价模型：

$\begin{align*} dS=\mu S dt+\sigma S dB① \end{align*}$

其中$\mu\,\sigma$是常数,$B$是布朗运动。
上述微分方程的解为：

$S\_{t}=S\_{0}exp\left[\sigma B\_{t}+\left( \mu -\sigma^{2}/2 \right)t \right]②$

对于欧式看涨期权，最终支付为$\left(S_{T}-X \right)^{+}$，所以有：

$V=e^{-r T}E\left[\left(S\_{T}-X\right)^{+}\right]③$

我们用②的模型：

$S\_{T}=S\_{0}exp\left[\sigma B\_{T}+\left( \mu -\sigma^{2}/2 \right)t \right]④$

由于$B_{T}$是服从均值为0，方差为T的正态分布，所以考虑用$\sqrt{T} Z$代替$B_{T}$,Z是标准正态分布：

$S\_{T}=S\_{0}exp\left[+\left(\sqrt{T} Z \mu -\sigma^{2}/2 \right)t \right]⑤$

则

$V=e^{-r T}E\left[\left(S\_{0}exp\left[+\left(\sqrt{T} Z \mu -\sigma^{2}/2 \right)t \right]-X\right)^{+}\right]⑥$

则有：

$V= \frac{e^{-r T}}{ \sqrt{2 \pi }} \int\_{- \infty }^{ \infty } \left{ \left(S\_{0}exp\left[+\left(\sqrt{T} Z \mu -\sigma^{2}/2 \right)t \right]-X\right)\right}^{+}e^{-x^{2}/2}dx⑦$

解方程$S_{0} e x p \left [ \sigma \sqrt{T} a+ \left(r- \frac{ \sigma^{2}}{2} \right) T \right ]-x=0$

得到：

$a= \frac{ \ln \left( \frac{X}{S\_{0}} \right)- \left(r- \frac{ \sigma^{2}}{2} \right) T}{ \sigma \sqrt{T}}$

接下来将⑦分为两部分求解，第二部分：

$\frac{1}{ \sqrt{2 \pi }} \int\_{a}^{ \infty } -X e^{-x^{2}/2} d x=-X N \left(-a \right)$

第一部分：

$\frac{1}{ \sqrt{2 \pi }} \int\_{a}^{ \infty } S\_{0} e x p \left [ \sigma \sqrt{T} x+ \left(r- \frac{ \sigma^{2}}{2} \right) T \right ] e^{-x^{2}/2} d x$

它等于：

$S\_{0} e^{r T} N \left(- \left(a- \sigma \sqrt{T} \right) \right)$

因此：
$V=S\_{0} N \left(- \left(a- \sigma \sqrt{T} \right) \right)-X e^{-r T} N \left(-a \right)$

这时之前求得的a值就有用了：
$a= \frac{ \ln \left( \frac{S\_{0}}{X} \right)+ \left(r- \frac{ \sigma^{2}}{2} \right) T}{ \sigma \sqrt{T}}$

$a= \frac{ \ln \left( \frac{S\_{0}}{X} \right)+ \left(r+ \frac{ \sigma^{2}}{2} \right) T}{ \sigma \sqrt{T}}$

令 $-a=d_{2}$ and $a- \sigma \sqrt{T}=d_{1}$,则有：

$V=S\_{0} N \left(d\_{1} \right)-e^{-r T} X N \left(d\_{2} \right)$

以上求解均假设没有分红，交易费用等。
对于欧式期权，BS公式有精确的定价公式，但对于美式期权，BS公式不可能求出解的表达式。

2.二叉树期权定价

二叉树也称为二项式定价模型，二项期权定价模型由考克斯（J.C.Cox）、罗斯（S.A.Ross）、鲁宾斯坦（M.Rubinstein）和夏普（Sharpe）等人提出的一种期权定价模型，主要用于计算美式期权的价值。其优点在于比较直观简单，不需要太多数学知识就可以加以应用。

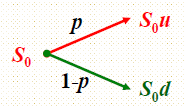
在很小的一段时间内假设股价会向上运动到$S_{0}u$,也可能向下运动到$S_{0}d$。
为了确定u，d，p，我们假设市场为风险中性，即股票预期收益率等于无风险利率，接着我们构造资产组合：
Portfolio：买$\Delta$单位的标的资产，卖出1单位的衍生品（期权）。
上涨情形：资产组合的价值为：

$S\_{0}u\Delta - f\_{u}$

下跌情形：资产组合的价值为：

$S\_{0}d\Delta - f\_{d}$

复制无风险资产，上述两式相等，可以解出：

$\Delta = \frac{f\_{u}-fsbtd}{S\_{0} u-S\_{0} d}$

再根据

$S\_{0} \Delta -f\_{0}= \left(S\_{0} u-f\_{u} \right) e^{-r T}$

求出

$f\_{0}=S\_{0} \Delta - \left(S\_{0} u \Delta -f\_{u} \right) e^{-r T}$

将$\Delta$代入得到

$f\_{0}=e^{-r T} \left [p f\_{u}+ \left(1-p \right) f\_{d} \right ]$

其中：
$p= \frac{e^{-r T}-d}{u-d}$

根据风险中性的假设，我们有如下方程组(均值和方差)：

$p u+ \left(1-p \right) d=e^{r\Delta t}$ $p u^{2}+ \left(1-p \right) d^{2}-e^{2 r \Delta t}= \sigma^{2} \Delta t$

再假设u=1/d，那么便可以解出p，u，d：

$u=e^{\sigma \sqrt \Delta t}$ $d=e^{- \sigma \sqrt \Delta t}$

以下是在matlab中实现的欧式期权二叉树定价，假设没有红利支付。可以用N来调节需要的二叉树的期数。

function [c1,p1]=bt(N)
%s0: stock price
%k: strik price
%sigma: volatility of stock
%r：riskfree rate
%T：expiration date

s0=99.62;
k=100;
sigma=0.4782;
r=0.0185;
T=0.2322;
dt=T/N;

u=exp(sigma*sqrt(dt));
d=1/u;

pu=(exp(r*dt)-d)/(u-d);
pd=(u-exp(r*dt))/(u-d);


c=0;
p=0;
for i =0:N
    s=s0*u^i*d^(N-i);
    c=c+max((s-k),0)*pu^i*nchoosek(N,i)*pd^(N-i);
    p=p+max((k-s),0)*pu^i*nchoosek(N,i)*pd^(N-i);
end

c1=c*exp(-r*T);
p1=p*exp(-r*T);

二叉树和BS公式定价的比较

可以证明，随着期数的增加，二叉树的结果收敛于BS公式的结果。

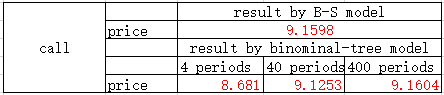
当然，二叉树也可以为美式期权定价，方法与欧式期权类似，只不过需要算出每个节点的价格，代码就不贴了，有兴趣可以自己实现以下。

3.蒙特卡洛模拟美式看跌期权定价——Regression-Based Methods

蒙特卡洛模拟可以轻松实现路径依赖期权（障碍期权、亚式齐全）的定价。近年来，由Longstaff和Schwartz提出的最小二乘蒙特卡洛(LSM)模拟方法，该方法已成为目前使用蒙特卡洛模拟美式期权定价的标准方法。LSM有这样一些假定：不支付交易费和税收、无套利机会、不支付红利、无风险利率是常数、标的资产价格演化遵循几何布朗运动。

基本思想： $V\_{ \imath } \left(s \right)=max \left{h\_{ \imath } \left(s \right) , E \left [V\_{ \imath +1} \left(S\_{ \imath +1} \right) | S\_{ \imath }=s \right ] \right}$ max里第一项是现在执行获得的payoff，第二项是选择等待所能获得的payoff的期望，这个期望用多项式回归的方法获得，即建立当期股价与下期payoff的模型。

import numpy as np
def regressionP(K,M=1000,N=50):
#lam: poisson分布的均值
#S：模拟的股价矩阵
#f：立即执行的payoff矩阵
#M：模拟的路径数量
#N：模拟的期数
    r=0.0173
    sigma=0.24722
    S0=96.10
    #K=97.50
    T=117.0/360 #单位是年
    lam=4
    dt=T/N
    S=np.zeros((M,N+1))
    S[:,0]=S0
    f=np.zeros\_like(S)
    f[:,0]=0

    #这里模拟股价矩阵用到了跳跃扩散过程，也可以试一下其它的
    X=np.random.poisson(lam*dt,(M,N))
    for i in range(M):
        for j in range(1,N+1):
            Y=1.1+0.2*np.random.rand(X[i,j-1])
            m=Y.prod()
            S[i,j]=S[i,j-1]*np.exp((r-0.5*sigma**2)*dt+sigma*dt**0.5*np.random.randn())*m
            f[i,j]=max(K-S[i,j],0)
    
    P=0 #期权价格
    y=np.zeros((M,N)) #最小二乘拟合的payoff
    d=np.zeros((M,1)) #用于计数，之后判断f矩阵中的值是不是每行第一个大于0的
    for i in range(1,N):
        a=f[:,i+1] #a，b是临时储存向量的变量（想不出什么好名字。。）
        b=S[:,i]
        
        W=a[f[:,i]>0]*np.exp(-r*dt)
        s=b[f[:,i]>0]
        #W是回归模型的因变量
        #s是回归模拟的自变量
        if s.size==0:
            pass
        else:
            z=np.polyfit(s,W,2) #这里建立的是二次多项式模型，试了下更高次的，结果区别不大
            p=np.poly1d(z)
            y[:,i]=p(b)
        
            f[:,i]=f[:,i]*((f[:,i]>y[:,i])*1)
        
        
            d=d+((f[:,i]>0)*1).reshape(M,1)
            q=f[:,i].reshape(M,1)
            P=P+sum(q[d==1])*np.exp(-r*dt*i)
            #这个地方的reshape折腾的死去活来。。
    
    #由于最后一列的f没有在上述循环里面，需要单独写出来
    d=d+((f[:,N]>0)*1).reshape(M,1)
    q=f[:,N].reshape(M,1)
    P=(P+sum(q[d==1])*np.exp(-r*T))/M
    return P

import warnings
warnings.filterwarnings("ignore")
p=[]
for i in np.arange(80,100,2.5):
    c=regressionP(i)
    p.append(c)
for i in np.arange(100,130,5):
    c=regressionP(i)
    p.append(c)
real=[1.01,1.23,1.65,2.18,2.58,3.67,4.70,6,7.5,11.47,15.65,19.30,24.15,29.60]
l1=np.arange(80,100,2.5)
l2=np.arange(100,130,5)
x=np.concatenate((l1,l2))


import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
plt.figure()
plt.plot(x,p,'k-',label='LSM method')
plt.plot(x,real,'k--',label='real price')
plt.ylabel('put option price')
plt.xlabel('strike price')
plt.legend(loc='best')
plt.show()

这里我选择苹果公司的股票和期权来进行定价。一般来讲，做模拟的话，深度实值或者深度虚值期权定价与实际价格的差距较大，越接近平值越准确。可是上图却好像是相反的，这是怎么回事，我也还没有想清楚，还请大神赐教。

4.有限差分

B-S partial differential equation

先来看一下BS偏微分方程（这个东西很让人头大啊。。）：

之前提过，股票的价格遵循几何布朗运动：

$dS=\mu S dt+\sigma S dB①$

$\mu$和$\sigma$表示股票价格的预期收益率和波动率。

$V \left(S , t \right)$表示某股票期权的价格，我们对它做泰勒展开(直接省略了大于2阶的项)：

$d V= \frac{ \partial V}{ \partial S} d S+ \frac{ \partial V}{ \partial t} d t+ \frac{1}{2 ^{ } } \frac{ \partial^{2} V}{ \partial S^{2}} \left( d S \right)^{2}+ \frac{ \partial^{2} V}{ \partial S \partial t} \left( d S d t \right)+ \frac{1}{2} \frac{ \partial^{2} V}{ \partial t^{2}} \left( d t \right)^{2}②$

将①代入②中，并只保留$dt$的一阶项：

$d V= \frac{ \partial V}{ \partial S} \left( \mu S d t+ \sigma S d B \right)+ \frac{ \partial V}{ \partial t} d t+ \frac{1}{2} ^{ } \frac{ \partial^{2} V}{ \partial S^{2}} \left( \mu S d t+ \sigma S d B \right)^{2}+ \frac{ \partial^{2} V}{ \partial S \partial t} \left( \mu S d t+ \sigma S d B \right) \left( d t \right)$

用$\sqrt{T} Z$代替$dB$,Z是标准正态分布，还是只保留一阶项：

$d V= \left( \frac{ \partial V}{ \partial t}+ \mu S \frac{ \partial V}{ \partial S}+ \frac{1}{2} \left( \sigma^{2} S^{2} Z^{2} \right) \frac{ \partial^{2} V}{ \partial S^{2}} \right) d t+ \sigma S \frac{ \partial V}{ \partial S} d B③$

为了简化上式，用$Z^{2}$的期望值代替它，$E \left(Z^{2} \right)=V a r \left(Z \right)=1$，进一步得到：

$d V= \left( \frac{ \partial V}{ \partial t}+ \mu S \frac{ \partial V}{ \partial S}+ \frac{1}{2} \left( \sigma^{2} S^{2} \right) \frac{ \partial^{2} V}{ \partial S^{2}} \right) d t+ \sigma S \frac{ \partial V}{ \partial S} d B④$

接下来考虑①式和③式离散的形式：

$\Delta S= \mu S \Delta t+ \sigma S \Delta B$ $\Delta V= \left( \frac{ \partial V}{ \partial t}+ \mu S \frac{ \partial V}{ \partial S}+ \frac{1}{2} \left( \sigma^{2} S^{2} \right) \frac{ \partial^{2} V}{ \partial S^{2}} \right) \Delta t+ \sigma S \frac{ \partial V}{ \partial S} \Delta B$

为了消除$\Delta B$，我们构建一个包含一单位衍生证券空头和$ \frac{ \partial V}{ \partial S}$，单位标的证券多头的投资组合，令$\Pi$为该组合的价值，则：

$\Pi =-V+ \frac{ \partial V}{ \partial S} S$

在经过$\Delta t$时间后，该资产组合的价值变化量为：

$\Delta \Pi =- \Delta V+ \frac{ \partial V}{ \partial S} \Delta S⑤$

将$Delta S$和$\Delta V$代入⑤式：

$\Delta \Pi =- \left( \frac{ \partial V}{ \partial t}+ \frac{1}{2} \frac{ \partial^{2} V}{ \partial S^{2}} \sigma^{2} S^{2} \right) \Delta t ⑥$

⑥式中不含$\Delta B$，因此在时间间隔$\Delta t$后该组合的价值必定无风险，其在$\Delta t$后的瞬时收益率一定等于无风险收益率，所以就有：$ \Delta \Pi =r \Pi \Delta t$，与⑥式联立整理后得到：

$\frac{ \partial V}{ \partial t}+r S \frac{ \partial V}{ \partial S}+ \frac{1}{2} \frac{ \partial^{2} V}{ \partial S^{2}} \sigma^{2} S^{2}=r V⑦$

这就是著名的BS偏微分方程，可以应用于价格取决于标的资产价格S的所有衍生证券定价。

用差分估计参数

终于搞定了PDE，现在就是要估计$\frac{ \partial V}{ \partial t}$，$\frac{ \partial V}{ \partial S}$ ，和$\frac{ \partial^{2} V}{ \partial S^{2}}$，于是就要用到差分的方法了：

$V\_{ \imath , j}=V \left( \imath \Delta t , j \Delta S \right) , \imath =0 , 1 , \dotsi , N , j=0 , 1 , \dotsi , M$

对于一阶项：

forward approximation： $ \frac{ \partial V}{ \partial S} \cong \frac{V_{ \imath , j+1}-V_{ \imath , j}}{ \Delta S}$，$ \frac{ \partial V}{ \partial t} \cong \frac{V_{ \imath +1 , j}-V_{ \imath , j}}{ \Delta t}$

backward approximation：$ \frac{ \partial V}{ \partial S} \cong \frac{V_{ \imath , j}-V_{ \imath , j-1}}{ \Delta S}$，$ \frac{ \partial V}{ \partial t} \cong \frac{V_{ \imath , j}-V_{ \imath -1 , j}}{ \Delta t}$

center approximation： $ \frac{ \partial V}{ \partial S} \cong \frac{V_{ \imath , j+1}-V_{ \imath , j-1}}{2 \Delta S}$，$ \frac{ \partial V}{ \partial t} \cong \frac{V_{ \imath +1 , j}-V_{ \imath -1 , j}}{2 \Delta t}$

二阶项：

$\frac{ \partial^{2} V}{ \partial S^{2}} \cong \frac{V\_{ \imath , j+1}+V\_{ \imath , j-1}-2 V\_{ \imath , j}}{ \Delta S^{2}}$

隐性差分

$\frac{ \partial V}{ \partial t} = \frac{V\_{ \imath +1 , j}-V\_{ \imath , j}}{ \Delta t}$ $\frac{ \partial V}{ \partial S} = \frac{V\_{ \imath , j}-V\_{ \imath , j-1}}{ \Delta S}$ $\frac{ \partial^{2} V}{ \partial S^{2}} = \frac{V\_{ \imath , j+1}+V\_{ \imath , j-1}-2 V\_{ \imath , j}}{ \Delta S^{2}}$

有了以上3个式子，再加上PDE，就可以得到下面的：

$a\_{j} f\_{ \imath , j-1}+b\_{j} f\_{ \imath , j}+c\_{j} f\_{ \imath , j+1}=f\_{ \imath +1 , j}$

可以得到$a_{j}$，$b_{j}$，$c_{j}$的通式(其中$ \frac{S}{ \Delta S}=j$)：

$a\_{j}= \frac{1}{2} \Delta t \left(r j- \sigma^{2} j^{2} \right)$ $b\_{j}=1+ \Delta t \left( \sigma^{2} j^{2}+r \right)$ $c\_{j}= \frac{-1}{2} \Delta t \left( \sigma^{2} j^{2}+r j \right)$

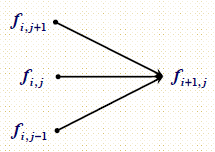
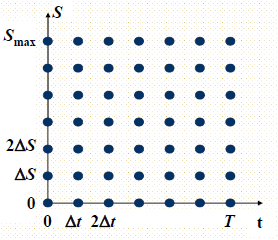
回想上面的网格图，以欧式看跌期权为例，算法如下：
1.初始化一些值，$f_{ \imath , 0}=K , f_{ \imath , M}=0 , f_{N , j}=m a x \left(K-j \Delta S , 0 \right)$，还有$a_{j}$，$b_{j}$，$c_{j}$。

2.for i =N:0，解方程组：

$a\_{1} f\_{ \imath -1, 0}+b\_{1} f\_{ \imath -1, 1}+c\_{1} f\_{ \imath -1, 2}=f\_{ \imath , 1}$ $a\_{2} f\_{ \imath -1, 1}+b\_{2} f\_{ \imath -1, 2}+c\_{2} f\_{ \imath -1, 3}=f\_{ \imath , 2}$ $\dotsi$ $a\_{M-1} f\_{ \imath -1, M-2}+b\_{M-1} f\_{ \imath -1, M-1}+c\_{M-1} f\_{ \imath -1, M}=f\_{ \imath , M}$

3.找到离S0最近的点，输出期权价格。

import numpy as np
from mpl\_toolkits.mplot3d import Axes3D
import seaborn as sns
import matplotlib.pyplot as plt

SMAX=150
dS=1
T=1
dT=0.1
K=50
r=0.1
sigma=0.5

N=T/dT
M=SMAX/dS

f=np.zeros((M+1,N+1))

f[0,:]=K
f[M,:]=0

f[:,N]=[max(K-j*dS,0) for j in range(M+1)]
a=[0.5*dT*(-sigma**2*j**2+r*j) for j in range(M-1)]
b=[1+dT*(sigma**2*j**2+r) for j in range(M-1)]
c=[-0.5*dT*(sigma**2*j**2+r*j) for j in range(M-1)]

x=np.zeros((M-1,M+1))
j=0
for i in range(M-1):
    x[i,j]=a[i]
    x[i,j+1]=b[i]
    x[i,j+2]=c[i]
    j+=1
x=x[:,1:M]
for i in np.arange(N,0,-1):
    y=f[:,i][1:M]
    f[:,i-1][1:M]=np.linalg.solve(x,y)


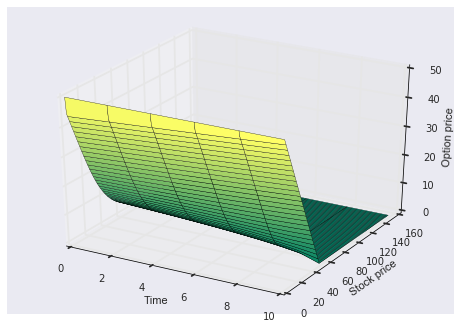
fig = plt.figure()
ax = fig.gca(projection='3d')
X,Y=np.meshgrid(np.arange(0,11,1),np.arange(0,151,1))
surf = ax.plot\_surface(X,Y,f, cmap='summer', cstride=2, rstride=2)
ax.set\_xlabel("Time")
ax.set\_ylabel("Stock price")
ax.set\_zlabel("Option price")

png