资产波动率及其模型

资产波动率是金融中最常用的风险度量。本章的目的是理解波动率的特点，学习波动率模型，并获取波动率建模和应用资产波动率的经验。
波动率在金融中有许多重要的应用。它是期权定价和资产分配中的一个关键因素。波动率在计算风险管理中的风险值（Value at Risk, VaR）时有重要作用。

4.1波动率的特征

存在波动率聚集(Volatility cluster)（即在某个特定时间段上波动率高，其他时间段上波动率较小）。
波动率随着时间的变化是连续的———波动率的跳跃式罕见的。
波动率不会散发到无穷———在一个固定的范围内变化。
存在杠杆效应(Leverage effect)，波动率一般对价格的大幅下降比上升更敏感。

一般有三种类型的波动率度量：

波动率是日收益率的条件标准差：这是波动率的常见定义。
隐含波动率：根据期权的价格用一个公式，如BS公式来推导出股票价格的波动率。
实际波动率：应用一天之内的高频数据来估计得到的日波动率。

4.2模型的结构

用rt表示某项资产在t时刻的对数收益率。波动率的基本思想是，序列{rt}是前后不相关或者低阶前后相关的，但序列不是独立的。

da=read.table("m-intcsp7309.txt",header=T)

intc=log(da$intc+1)
rtn=ts(intc,frequency=12,start=c(1973,1))
plot(rtn,type='l',xlab='year',ylab='ln-rtn')

t.test(intc)  # 检验收益率是否为0
Box.test(intc,lag=12,type='Ljung') #混成检验接受原假设——序列不相关

par(mfcol=c(2,1))
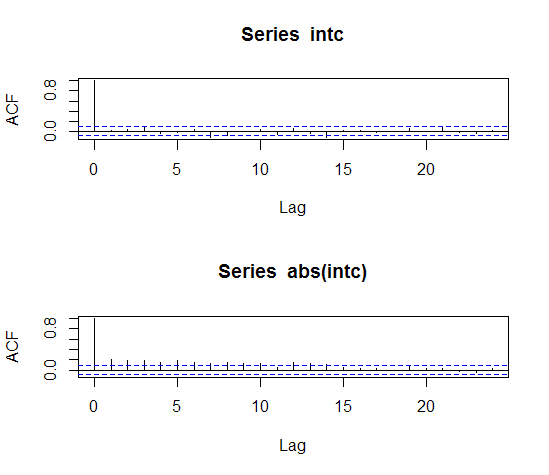
acf(intc,lag=24) # ACF plots
acf(abs(intc),lag=24) 
Box.test(abs(intc),lag=12,type='Ljung')#拒绝原假设——序列相关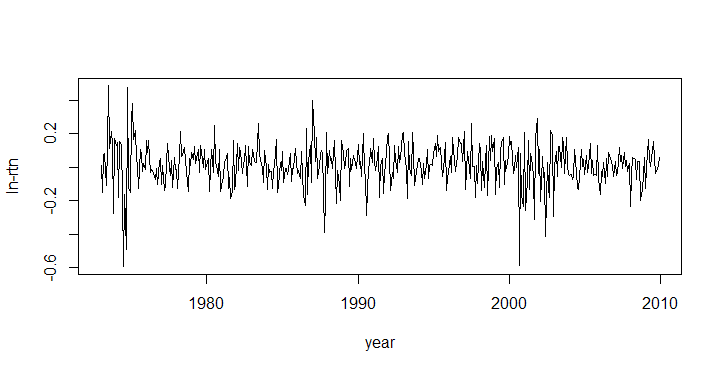

4.3模型的建立

对波动率建立方程需要如下4个步骤： 1. 通过检验序列的前后相关性来简历一个均值方程，消除线性依赖； 2. 对均值方程的残差进行ARCH效应检验； 3. 如果ARCH效应显著，制定一个波动率模型，并对均值方程和波动率方程进行联合估计； 4. 检查模型并改进。

4.4ARCH效应的检验

所谓ARCH效应，简单说就是用均值方程的残差的平方来近似波动率，看其自相关函数是否显著，若显著不为0则可以认为其存在ARCH效应。

y=intc-mean(intc)
Box.test(y^2,lag=12,type='Ljung')

$output
Box-Ljung test

data:  y^2
X-squared = 92.939, df = 12, p-value = 1.332e-14

可以看到P值非常显著，即显著不为0，则认为这个序列有ARCH效应。

4.5ARCH模型

ARCH模型的基本思想：

资产收益率的扰动序列yt是前后不相关的，但不独立；
yt的不独立性可以用其滞后值的简单二次函数来描述。

4.5.1ARCH模型的性质

下面是一个ARCH(1)模型：

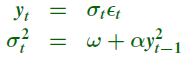
性质：

yt的无条件均值仍然是0，
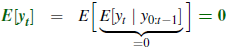
yt的无条件方差：

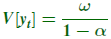
4.5.2ARCH模型的优点和缺点

优点：

该模型可以产生波动率聚集；
模型的扰动yt有厚尾部。

缺点：

无法产生波动率聚集；
对参数的限制相当强；
波动率的预报值会偏高。

4.5.3Intel股票月对数收益率的例子

通过yt^2的PACF定阶，先建立一个ARCH(3)模型
r_{_t} = μ+y_{_t}
y_{_t} = σ_{_t}ε_{_t}
σ_{_t}² = ω+α_₁y_{_t−1}²+α_₂y_{_t−2}²+α_₃+y_{_t−3}²

library(fGarch) # Load package 
da=read.table("m-intcsp7309.txt",header=T)

intc=log(da$intc+1)
m1=garchFit(~1+garch(3,0),data=intc,trace=F)#fit model
summary(m1)

$output
Title:
 GARCH Modelling 

Call:
 garchFit(formula = ~1 + garch(3, 0), data = intc, trace = F) 

Mean and Variance Equation:
 data ~ 1 + garch(3, 0)
<environment: 0x00000000123ff268>
 [data = intc]

Conditional Distribution:
 norm 

Coefficient(s):
      mu     omega    alpha1    alpha2    alpha3  
0.012567  0.010421  0.232889  0.075069  0.051994  

Std. Errors:
 based on Hessian 

Error Analysis:
        Estimate  Std. Error  t value Pr(>|t|)    
mu      0.012567    0.005515    2.279   0.0227 *  
omega   0.010421    0.001238    8.418   <2e-16 ***
alpha1  0.232889    0.111541    2.088   0.0368 *  
alpha2  0.075069    0.047305    1.587   0.1125    
alpha3  0.051994    0.045139    1.152   0.2494    
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

可以看到alpha2和alpha3的系数不显著，所以重新拟合一个ARCH(1)模型：

m2=garchFit(~1+garch(1,0),data=intc,trace=F)
summary(m2)

$output
Title:
 GARCH Modelling 

Call:
 garchFit(formula = ~1 + garch(1, 0), data = intc, trace = F) 

Mean and Variance Equation:
 data ~ 1 + garch(1, 0)
<environment: 0x000000001146bf78>
 [data = intc]

Conditional Distribution:
 norm 

Coefficient(s):
      mu     omega    alpha1  
0.013130  0.011046  0.374976  

Std. Errors:
 based on Hessian 

Error Analysis:
        Estimate  Std. Error  t value Pr(>|t|)    
mu      0.013130    0.005318    2.469  0.01355 *  
omega   0.011046    0.001196    9.238  < 2e-16 ***
alpha1  0.374976    0.112620    3.330  0.00087 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

现在模型的系数全部显著。

4.6GARCH模型

GARCH(1,1)=ARCH(oo)
GACH(1,1)模型等价于无穷阶的ARCH模型，其形式如下：
r_{_t} = μ+y_{_t}
y_{_t} = σ_{_t}ε_{_t}
σ_{_t}² = ω+αy_{_t−1}²+βσ_{_t−1}²

4.6.1实例说明

ARCH模型的建模过程也适用于GARCH模型。一般GARCH(1,1)就够用了。

library(fGarch)
m4=garchFit(~1+garch(1,1),data=intc,trace=F)
summary(m4)

v1=volatility(m4)  # Obtain volatility
resi=residuals(m4,standardize=T) # Standardized residuals
vol=ts(v1,frequency=12,start=c(1973,1))
res=ts(resi,frequency=12,start=c(1973,1))
par(mfcol=c(2,1))  # Show volatility and residuals
plot(vol,xlab='year',ylab='volatility',type='l')
plot(res,xlab='year',ylab='st. resi',type='l')

$output
Coefficient(s):
        mu       omega      alpha1       beta1  
0.01126568  0.00091902  0.08643831  0.85258554  

Std. Errors:
 based on Hessian 

Error Analysis:
        Estimate  Std. Error  t value Pr(>|t|)    
mu     0.0112657   0.0053931    2.089  0.03672 *  
omega  0.0009190   0.0003888    2.364  0.01808 *  
alpha1 0.0864383   0.0265439    3.256  0.00113 ** 
beta1  0.8525855   0.0394322   21.622  < 2e-16 ***

可以看到系数都显著，下面是波动率序列和残差序列：

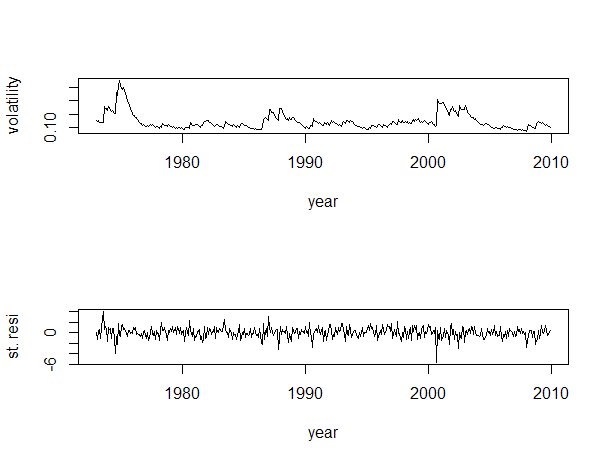
par(mfcol=c(2,2)) # Obtain ACF & PACF
acf(resi,lag=24)
pacf(resi,lag=24)
acf(resi^2,lag=24)
pacf(resi^2,lag=24) 
#绘制at和at^2的ACF和PACF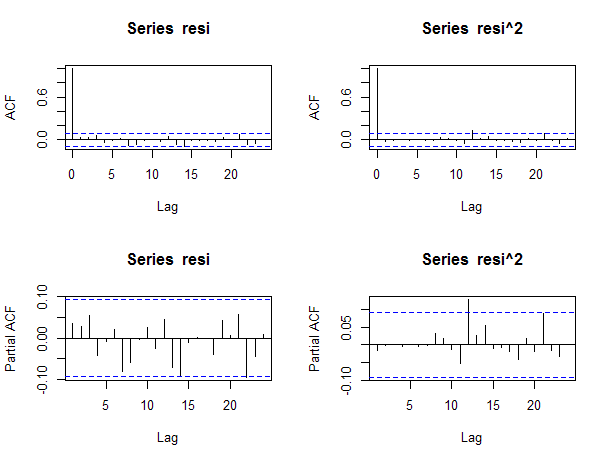

这些ACF和PACF确认了拟合模型充分刻画了对数收益率序列的条件均值和方差。

4.7指数GARCH模型

Nelson(1991)提出了指数GARCH模型(EGARCH)模型。具体地，为了允许在模型中体现正的和负的资产收益率的非对称效应，形式如下：

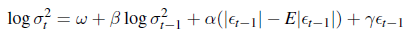
能体现杠杆效应的还有TGARCH、APGARCH等。

Akuan

面白い人間になりたい