金融时间序列的线性模型

2.1平稳性

如果一个时间序列满足：

均值是常数
方差存在且为常数
协方差只与时间间隔有关，与时间无关

则它是弱平稳的。

2.2相关系数和自相关函数

皮尔逊相关系数：

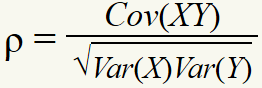
da=read.table("m-ibmsp6709.txt",header=T)
head(da)
ibm=da$ibm
sp5=da$sp
cor(sp5,ibm)
cor(sp5,ibm,method='spearman')
cor(sp5,ibm,method='kendall')

自相关函数：

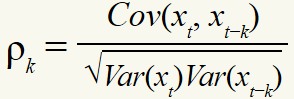
一个弱平稳时间序列x_{_t}是序列自身前后不相关的。

da=read.table("m-dec12910.txt",header=T)
d10=da$dec10  # select the Decile 10 returns
dec10=ts(d10,frequency=12,start=c(1967,1))
par(mfcol=c(2,1))
plot(dec10,xlab='year',ylab='returns')
title(main='(a): Simple returns')
acf(d10,lag=24) # command to obtain sample ACF of the data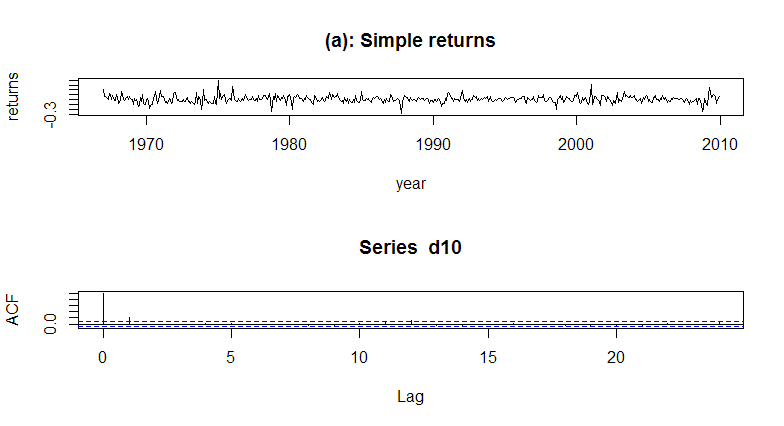

混成检验

一个线性时间序列模型可以完全由其ACF来刻画，我们经常需要联合检验x_{_t}的多个自相关系数是否同时为0，Box和Pierce提出了混成统计量，R里用Box.test来实现：

da=read.table("m-ibmsp6709.txt",header=T)
ibm=da$ibm
lnibm=log(ibm+1) # Transfer to log returns
Box.test(ibm,lag=12,type='Ljung')
Box.test(lnibm,lag=12,type='Ljung')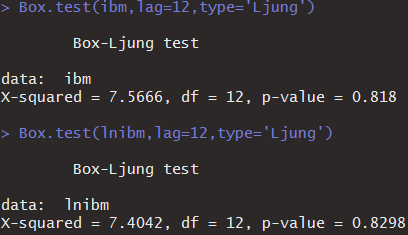

可以看到P值不显著，则接受原假设，即自相关函数为0.

2.3白噪声

白噪声：具有有限均值和有限方差的独立同分布的时间序列。
高斯白噪声：一个服从均值为0、方差有限的白噪声序列。

2.4简单自回归模型（AR）

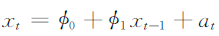
2.4.1AR模型的性质

均值：
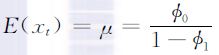
方差：
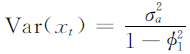
平稳的充要条件：
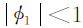
自相关系数：呈现漂亮的指数衰减。

2.4.2实践中AR模型的识别

AR(p)序列的的样本偏自相关函数是p步截尾的。

2.5简单移动平均模型（MA）

MA(1)模型的一般形式为：

2.5.1MA模型的性质

MA模型的常数项就是序列的的均值
MA(q)模型的方差为
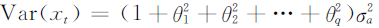
自相关函数（ACF）
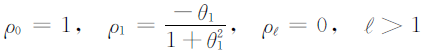
MA(q)序列只与其前q个滞后值线性相关，是一个“有限记忆”模型。

2.5.2MA模型定阶

简单的说，MA(q)模型的ACF是q阶截尾的。

2.6简单ARMA模型

ARMA(1,1)模型的形式：

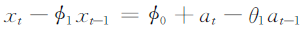
2.6.1ARMA(1,1)模型的性质

均值：
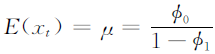
方差：
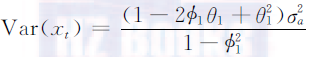
ACF和PACF都不能在任意有限间隔后截尾
ACF与AR(1)模型很相似，只是指数衰减从间隔2开始。
PACF与MA(1)模型很相似，只是指数衰减从间隔2开始。

2.6.2ARMA模型的识别

ACF和PACF都无法提供足够的信息来识别ARMA模型，这时可以用到推广的自相关函数（EACF）。

2.7单位根非平稳型

利率、汇率、资产的价格序列往往都是非平稳的，这样的非平稳序列叫做单位根非平稳时间序列（unit-root nonstationary time series）。

2.7.1随机游走

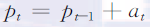
它可以被看作一个特殊的AR(1)模型，那么p_{_t-1}的系数是1，这不满足AR(1)的平稳性条件。从而随机游走不是弱平稳的。

2.7.2带漂移的随机游走

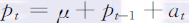
常数项表示价格的时间趋势，通常称为模型的漂移（drift）。

常数项的解释：

对于MA(q)模型，常数项就是序列的均值；
对于AR(p)和ARMA(p,q)模型，常数项与均值有关；
对带漂移的随机游走，常数项变为序列的时间斜率。

2.7.3单位根检验

原假设：有单位根p_{_t-1}的系数为1；备择假设：其系数小于1.

利用如下两个模型：

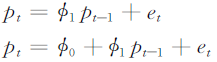
DF统计量为：

由于经常使用的是AR(p)模型，所以需要用到扩展DF单位根(Augmented Dickey-Fuller, ADF)检验。

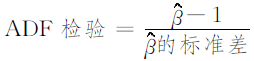
library(fUnitRoots)
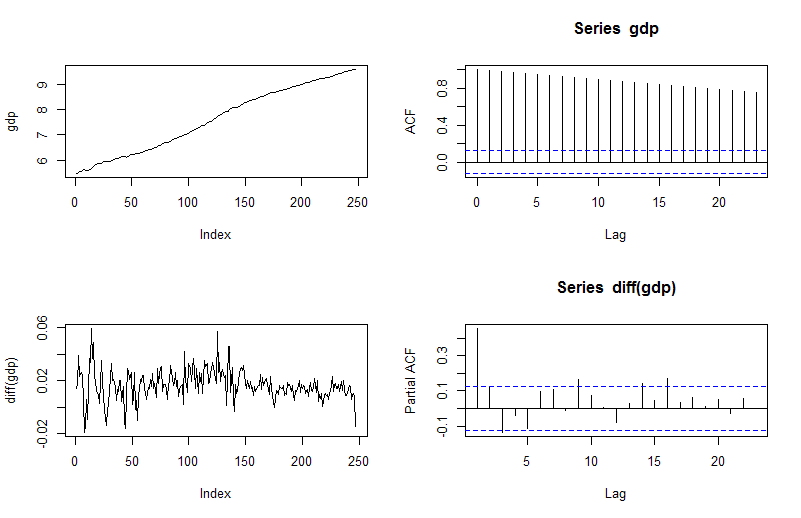
da=read.table("q-gdp4708.txt",header=T)
gdp=log(da[,4])
m1=ar(diff(gdp),method='mle')
adfTest(gdp,lags=10,type=c("c"))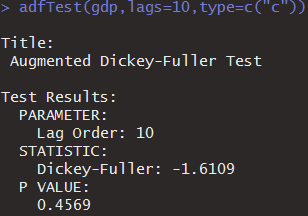

p值可以看出接受原假设，即存在单位根。

Akuan

面白い人間になりたい